Hill Climbing in Artificial Intelligence

 

Hill Climbing Algorithm

•      Hill Climbing is a technique to solve certain optimization problems.

•      In these techniques, we start with a sub-optimal solution, which is improved repeatedly until some condition is maximized.

•      The idea of starting with a sub-optimal solution is compared to walking up the hill, and finally maximizing some condition is compared to reaching the top of the hill.

Algorithm:

1) Evaluate the initial state. If it is goal state then return and quit.

2) Loop until a solution is found or there are no new operators left.

3) Select & apply a new operator.

4) Evaluate new state 

If it is a goal state, then quit.

If it is better than the current state then make it a new current state.

If it is not better than the current then go to step 2.

It is so-called because of the way the nodes are selected for expansion. At each point search path, the successor node that appears to lead most quickly to the top of the hill is selected for exploration. It terminates when it reaches a “peak” where no neighbor has a higher value. This algorithm doesn’t maintain a search tree so the data structure for the current node need only record the state and the value of the objective function. The Hill Climbing Algorithm is sometimes called as a greedy local search because it grabs a good neighbor state without thinking ahead about where to go next. Unfortunately, hill climbing suffers from the following problems:

Fig. 1.1  Hill Climbing

·     Local maxima:

A local maximum is a state which is better than its neighbor states, but there is also another state which is higher than it. They are also called foot-hills. It is shown in Fig. 1.2

Fig. 1.2 Local maximum or foothill

A solution to this problem:

The backtracking technique can be a solution of the local maximum in-state space landscape. Create a list of the promising paths so that the algorithm can backtrack the search space and explore other paths.

·     Plateau:

It is a flat area of the search space in which a whole set of neighboring states (nodes) have the same heuristic value. A plateau is shown in Fig. 1.3 

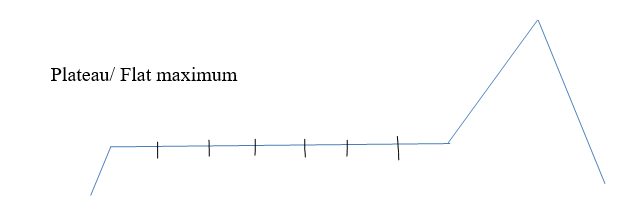
Fig. 1.3 Plateau

A solution to this problem:

The solution for the plateau is to take big steps or very little steps while searching, to solve the problem. Randomly select a state that is far away from the current state so it is possible that the algorithm could find a non-plateau region.

Another solution is to apply small steps several times in the same direction.

·     Ridge:

It’s an area which is higher than surrounding states but it cannot be reached in a single move. It is an area of the search space that is higher than the surrounding areas and that itself has a slope. Ridge is shown in Fig. 1.4 

Fig. 1.4 

A solution to this problem:

Trying different paths at the same time is a solution. With the use of bidirectional search, or by moving in different directions, we can improve this problem.

Advantages of Hill Climbing:

It can be used in continuous as well as discrete domains.

Hill climbing typically requires minimal memory, making it suitable for resource-constrained environments.

Hill climbing is easy to understand and implement.

Hill climbing can be adapted to different problem domains by modifying the objective function and search space representation.

Disadvantages of Hill Climbing:

Hill climbing tends to get stuck in local optima, which are solutions that are better than their immediate neighbors but not necessarily the global optimum.

It is not suitable for those problems whose value of the heuristic function drops off suddenly when a solution may be in sight.

It is a local method as it looks at the immediate solution and decides about the next step to be taken rather than exploring all consequences before taking a move.

The quality of the solution found by hill climbing heavily depends on the initial solution or starting point. If the initial state is far from the global optimum, the algorithm may not reach the best solution.